用PyWavelets学习小波变换

基础概念

离散小波变换（DWT）

傅里叶变换可以提取出一组数据中的频域信息，我们可以通过变换+修改频域+逆变换实现对高频（低频）的移除。其局限性是只能处理周期性的数据，这是由于其基函数是一个周期性的函数导致。

小波变换则可以处理非周期性的数据，因为其基函数是一个仅在很小的范围内非零，且均值是零的函数，因此可以组合出非周期性的数据。

离散小波变换是针对一个一个的非连续（即离散）的数据进行变换，工程中遇到的数据都是离散的。

关于DWT的更多信息，可参考：wikipedia

初尝：使用小波降噪

操作步骤

1. 对一个时间序列数据进行小波变换，得到近似系数（cA）和细节系数（cD）
2. 处理掉细节系数（cD），例如减半，或全部置零
3. 使用逆向变换即可得到去噪后数据。

代码实现

小波的种类有很多，在使用上，我们必须指出具体使用哪一种，这里我们先采用 db3.。

import pywt

# 原始数据（随机写的一组数）
m = [10, 14, 18, 17, 16, 29, 12, 24, 19, 29, 26, 20, 18, 19, 16, 18]

# 小波变换
cA, cD = pywt.dwt(m, 'db3')  # 'db3' 为一种具体的小波

# 处理 cD （分别取 cD=cD/2 和 cD=0）
cD2 = [i/2 for i in cD]
cD0 = [0 for i in cD]

# 逆向小波变换
n2 = pywt.idwt(cA, cD2, 'db3')
n0 = pywt.idwt(cA, cD0, 'db3')

效果比较

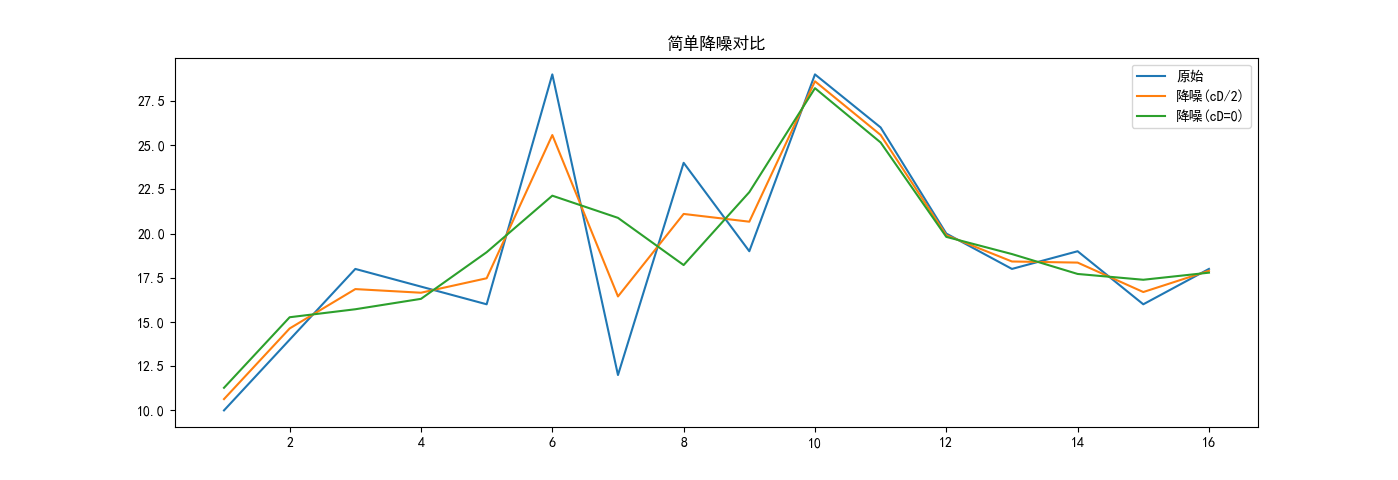
在同一个坐标系中绘制 m、n2、n0 三条线，可以看出经过“降噪”处理的值比原始m更加平滑。同时 把 cD 直接改为 0（绿色） 比 cD 降为原来的一半（橙色）更加平滑。

探究小波族

在简单粗暴法中，我们随便选取了一个小波族（db3），使用其进行了小波变换，PyWavelets 内置了 14 个小波族，每个族又可以细分为多种小波。具体列表如下：

>>> pywt.families()
['haar', 'db', 'sym', 'coif', 'bior', 'rbio', 'dmey', 'gaus', 'mexh', 'morl', 'cgau', 'shan', 'fbsp', 'cmor']

其中适用于 DWT 的小波列表如下：

>>> print(pywt.wavelist(kind='discrete'))
['bior1.1', 'bior1.3', 'bior1.5', 'bior2.2', 'bior2.4', 'bior2.6', 'bior2.8', 'bior3.1', 'bior3.3', 'bior3.5', 'bior3.7', 'bior3.9', 'bior4.4', 'bior5.5', 'bior6.8', 'coif1', 'coif2', 'coif3', 'coif4', 'coif5', 'coif6', 'coif7', 'coif8', 'coif9', 'coif10', 'coif11', 'coif12', 'coif13', 'coif14', 'coif15', 'coif16', 'coif17', 'db1', 'db2', 'db3', 'db4', 'db5', 'db6', 'db7', 'db8', 'db9', 'db10', 'db11', 'db12', 'db13', 'db14', 'db15', 'db16', 'db17', 'db18', 'db19', 'db20', 'db21', 'db22', 'db23', 'db24', 'db25', 'db26', 'db27', 'db28', 'db29', 'db30', 'db31', 'db32', 'db33', 'db34', 'db35', 'db36', 'db37', 'db38', 'dmey', 'haar', 'rbio1.1', 'rbio1.3', 'rbio1.5', 'rbio2.2', 'rbio2.4', 'rbio2.6', 'rbio2.8', 'rbio3.1', 'rbio3.3', 'rbio3.5', 'rbio3.7', 'rbio3.9', 'rbio4.4', 'rbio5.5', 'rbio6.8', 'sym2', 'sym3', 'sym4', 'sym5', 'sym6', 'sym7', 'sym8', 'sym9', 'sym10', 'sym11', 'sym12', 'sym13', 'sym14', 'sym15', 'sym16', 'sym17', 'sym18', 'sym19', 'sym20']

每种小波的介绍可以参考：有关小波的几个术语及常见的小波基介绍

参考资料

• PyWavelets Wavelet Transforms in Python
• https://blog.csdn.net/nanbei2463776506/article/details/64124841
• 基于小波变换的时间序列降噪
• Python中 pywt 小波分析库中的一些基本使用方法
• Python小波变换去噪
• 小波变换（wavelet transform）的通俗解释（一）
• 有关小波的几个术语及常见的小波基介绍
• 如何通俗地讲解傅立叶分析和小波分析间的关系？
• The Wavelet Tutorial
• WAVELETS FOR KIDS
• 小波变换和motion信号处理-1 2 3
• Matlab Wavelet Toolbox
• 有关小波的几个术语及常见的小波基介绍